Cours MAP572 2011

De Wikimacs.

Sommaire

Electromagnétisme et Acoustique dans l'industrie aéronautique et automobile : de la modélisation au calcul haute performance

Aller à


Objectifs du cours

Cet enseignement d'approfondissement présente deux méthodes numériques largement diffusées dans le monde industriel pour la résolution des phénomènes de propagation d'ondes, la méthode des différences finies et la méthode des éléments finis de frontière. Nous en présenterons des applications industrielles comme la réduction du bruit des avions ou des voitures, la Compatibilité Electromagnétique qui permet d'assurer le bon fonctionnement des systèmes électriques embarqués, l'installation des antennes afin d'assurer une bonne couverture et diminuer les effets parasites de couplages entre antennes.

Modèle FDTD d'un AIRBUS A380 en vue d'un calcul somulation des effets indirects de la foudre - (c) EADS Innovation Works


Même si les deux physiques concernées semblent très éloignées l'une de l'autre, une approche commune mathématique et numérique permet de mutualiser les développements numériques et la compréhension des notions clés : causalité et condition de radiation, dispersion numérique, écriture sous forme intégrale des équations...

Calcul BEM FMM de la diffraction d'une onde électromagnétique par un modèle d'entrée d'air - (c) EADS Innovation Works

Le cours est composé de séances magistrales introductives permettant d'aborder la modélisation théorique et numérique, de séances en petits groupes pour analyser le cas simplifié mais très instructif de la dimension 1, des séances pratiques permettant d'utiliser des logiciels industriels dans un contexte tridimensionnel. Un polycopié est disponible rassemblant l'ensemble des résultats utiles.


Tyre-road noise : Calcul BEM de la fonction de transfert temporelle - (c) PSA Peugeot Citrën

Des projets de modélisation numérique seront proposés aux élèves consistant en une étude voisine du travail d'un ingénieur d'étude en milieu industriel.


Modalités d'évaluation : Un projet de modélisation numérique et une évaluation de la présence et du travail fourni en séance.

Le cours aura lieu en PC72 de 13h30 à 18h.

1ère séance : introduction (20/09/11)

Présentation du cours

  1. Fonctionnement du cours :
    • Introduction des notions de base sous forme de cours magistraux en début de séance.
    • Approfondissement de différents sujets sous forme de feuilles d'excercices et de projets à réaliser en binôme avec utilisation d'un logiciel industriel.
    • Présentations régulières de l'avancement des projets et complément par les enseignants.
  2. Présentation du contexte industriel, motivation, méthodes numériques utilisées dans l'industrie.
  3. Présentation des projets. Formation des binômes et installation des logiciels à faire rapidement.
  4. Présentation du polycopié et guide de lecture.

Modélisation, équation des ondes

  1. D’Alembert §2.2.1 et §2.2.2. Feuille d'exercice No. 1 - exo 1
  2. Energie §2.2.4 Feuille d'exercice No. 1 - exo 2

2ème séance : solutions explicites (27/09/11)

Cours :

Cette séance est consacrée au calcul de quelques solutions explicites d’équations d’onde, en particulier les solutions élémentaires de ces équations. Ceci permet d’introduire naturellement des notions importantes comme la causalité et la condition de radiation, puis de poser le problème dediffraction.

  • Solutions du problème homogène dans 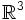\mathbb R ^3 considéré homogène
    1. Ondes planes en électromagnétisme : domaines temporel et fréquentiel (Formules de calcul vectoriel). §1.3.2
    2. Ondes sphériques scalaires (Nous verrons plus loin qu’il s’agit d’intégrales d’ondes planes). §1.3.3
    3. Notions de causalité et condition de radiation de Sommerfeld §1.3.3
  • Solution élémentaire pour l’équation des ondes scalaire §3.2.1
    1. Rappel de la solution élémentaire du Laplacien
    2. Calcul de la solution élémentaire de l’équation de Helmholtz.
    3. Solutions générales de l'équation de Helmholtz dans l'espace libre
  • Définition du problème de diffraction §1.3.4
    1. Définition d’un obstacle : perturbation du milieu homogène infini
    2. Onde incidente : solution dans tout l’espace de l’équation avec second membre (terme source)
    3. Onde diffractée : perturbation de l’onde incidente par la présence de l’obstacle

TD : Equation des ondes 1D (suite)

  1. Refaire le cône de dépendance et CFL (voir D'Alembert) + énergie
  2. Fonction de Green §2.4.1 et §2.4.2 Feuille d'exercice No. 1 - exo4 + Cas d'une équation différentielle ordinaire.

(à proposer comme travail personnel ?) :

  1. Analyse du pb de transmission Compléments à la feuille d'exercice 1
  2. Principe des images §2.5.1 et §2.5.2 Feuille d'exercice No. 1 - exo5

3ème séance : Existence et unicité pour le problème de diffraction (04/10/11)

TD : Analyse de problème de diffraction et transmission 1D temporel

  1. Principe des images §2.5.1 et §2.5.2 Feuille d'exercice No. 1 - exo5
  2. Analyse du pb de transmission Compléments à la feuille d'exercice 1

Cours

  • Résolution explicite pour la symétrie sphérique
    1. Harmoniques sphériques §3.3.1


4ème séance : Existence et unicité pour le problème de diffraction(fin) Représentation des solutions dans l’espace libre (11/10/11)

Cours

  • Résolution explicite pour la symétrie sphérique
    1. Résolution du problème de Dirichlet §3.3.2 et §3.3.3
    2. Opérateur de Dirichlet-Neumann §3.3.4
  • Eléments pour l'analyse du problème de diffraction fréquentiel
    1. Définition d'un problème dans un domaine tronqué équivalent au problème de diffraction fréquentiel §3.4.3
    2. Formulation variationnelle du problème dans le domaine tronqué. §3.4.4
    3. Principe de la preuve d'existence et unicité. §3.4.4
  • Principes généraux de la méthode des équations intégrales
    1. Fonction de Green
    2. Solution dans l'espace libre
    3. Formule de représentation intégrale
    4. Conditions aux limites et équation intégrale
    5. Formulation variationnelle
    6. Approximation variationnelle - éléments finis de frontière

TD

Equations intégrales en 1D : première partie de l'examen 2008

5ème séance : Représentation des solutions dans l’espace libre (18/10/11)

Cours

  • Principes généraux de la méthode des équations intégrales
    1. Fonction de Green
    2. Solution dans l'espace libre
    3. Formule de représentation intégrale
    4. Conditions aux limites et équation intégrale
    5. Formulation variationnelle
    6. Approximation variationnelle - éléments finis de frontière
  • Théorème de représentation intégrale
    1. Représentation de la pression solution équation de Helmholtz
    2. définition potentiels simple et double couche
    3. problématique des traces des potentiels sur le bord. OK pour la trace 0, à faire pour la trace 1 (dérivée normale)
    4. remarque sur la singularité des noyaux

TD

TD : Analyse de problème de diffraction 3D

  1. Dipôles électriques et magnétiques §3.2.2 Feuille d'exercice No. 2 - exo1
  2. Solutions explicites avec symétrie sphérique §3.3.2, §3.3.3 et §3.3.4 Feuille d'exercice No. 2 - exo2
  3. Solution élémentaire de l'équation de Helmholtz en 3D §3.2.1 Feuille d'exercice No. 2 - exo3
  • Rayonnement de sources dans l'espace libre §5.3
    1. Rappels sur les solutions élémentaires et leur utilisation
    2. Deux approches possibles : équation du second ordre (Helmholtz en p) ou le système du second ordre équivalent (acoustique en p et V)
    3. Sources ponctuelles, convolution et translation. Relation entre le rayonnement d'une source de force et une source de débit dipolaire

6ème séance : Représentation intégrale & équations intégrales (15/11/09)

Cours

  • Rappels séance précédente et commentaires sur la formule de représentation intégrale :
    1. c'est l'intégrale sur une surface du rayonnement d'une densité de monopôles et de dipôles. Ceci conduit à introduire les distributions de simple et double couche :
      • distribution de simple couche : densité surfacique de monopôles
      • distribution de double couche : c'est la densité surfacique de dipôles

Lien avec les monopôles et dipôles

  • Rayonnement de sources ponctuelles, volumiques et surfaciques
    1. Sources ponctuelles, convolution et translation. Relation entre le rayonnement d'une source de force et une source de débit dipolaire
    2. Sources volumiques, même remarque que précédemment entre le rayonnement des sources de l'équation de Helmholtz et celles du systme de l'acoustique. Intégration par partie pour reporter un rot sur la densité de force
    3. Sources surfaciques de type potentiel de simple couche : énoncé et propriétés.
    4. Idem pour les sources surfaciques de type potentiel de double couche. Ne pas rentrer dans un discours sur les opérateurs différentiels surfaciques. Dire juste que la formule avec le rot surfacique et la généralisation au 3D d'une dérivée par rapport à l'abscisse curviligne si Γ était une courbe en 2D ;
  • Théorème de représentation intégrale (nouvelle preuve et suite)
    1. Lemme des sauts (rappel 1D et 3D pour la dérivée 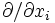\partial / \partial x_i, énoncé sans preuve de la formule pour le Laplacien)
    2. Représentation de p et V
    3. Traces. Notations 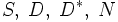S,\; D,\; D^*,\; N et écriture matricielle des traces.
  • Equations intégrales
    1. Prolongement arbitraire  : n'a pas influence (en théorie) sur la solution dans le domaine extérieur (cf. théorème de représentation intégrale)
    2. Problème de Dirichlet extérieur avec prolongement continu

(fait rapidement)

TD

Feuille d'exercice No. 4  :

  • Exo 1 : Asymptotique champ lointain ;
  • Exo 2 : Projecteur de Calderón

7ème séance : Equations intégrales (22/11/11)

Cours

  • Equations intégrales
    1. Inversibilité des opérateurs intégraux
    2. Problème de Dirichlet et Neumann extérieur (simple/double couche). Formulation variationnelle pour S.

TD

7ème séance : Méthode des différences finies en domaine temporel (04/11/09)

Cours

  • Première analyse sur le cas simplifié de la dimension 1
    1. Le schéma saute-mouton §4.2.3
    2. Vitesse de propagation numérique. Condition nécessaire de convergence §4.2.4
    3. Identité d'énergie §4.2.5
  • Schéma FDTD pour le système de Maxwell en dimension 3
    1. Le schéma de Yee §4.3.1
    2. Propriétés discrètes du schéma de Yee §4.3.2
    3. Analyse de stabilité §4.3.2 et §4.3.3

TD : Quelques propriétés du schéma aux différences finies

  1. Dispersion numérique §4.2.7 et §4.3.3 Feuille d'exercice No. 3 - exo1
  2. Analyse des θ-schémas Feuille d'exercice No. 3 - exo2

8ème séance : TP FDTD (29/11/11)

9ème séance : BEM, temporel et FMM (06/12/11)

Cours

  • BEM
    1. Simple couche en P0 : matrice symétrique complexe, complexité, mémoire...
    2. Neumann double couche : rappeler la formulation variationnelle -> nécessité d'une discrétisation en P1 (au moins) continue.

Perspectives

  • Méthode des potentiels retardés
  • Multipôles rapides (FMM) : planches d'IT
  • Exemples d'applications : simulation en acoustique automobile

10ème séance : Examen (date à préciser)

Présentation des projets par les binômes. Présence de tous obligatoire.

Récupérée de « http://imacs.polytechnique.fr/wikimacs/index.php/Cours_MAP572_2011 »
Outils personnels