De Wikimacs.

Version du 8 octobre 2007 à 20:48

Organisation du cours 2007-2008

Aller à

• Page officielle du cours pour le résumé

Séance 2 : solutions explicites

Cours (§3.2 et §3.3 du poly)

Cette séance est consacrée au calcul de quelques solutions explicites d’équations d’onde, en particulier les solutions élémentaires de ces équations. Ceci permet d’introduire naturellement des notions importantes comme la causalité et la condition de radiation.

• Formule de D’Alembert en dimension 1 d’espace

Il s'agit essentillement d'un rappel 1ère séance : c'est le premier exemple de solution explicite dans tout l’espace, puis d'une solution du problème de Cauchy.

• Solutions du problème homogène dans 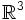considéré homogène
  1. Ondes planes en électromagnétisme : domaines temporel et fréquentiel (Formules de calcul vectoriel).
  2. Ondes sphériques scalaires (Nous verrons plus loin qu’il s’agit d’intégrales d’ondes planes).
  3. Notions de causalité et condition de radiation de Sommerfeld
• Définition du problème de diffraction
  1. Définition d’un obstacle : perturbation du milieu homogène infini
  2. Onde incidente : solution dans tout l’espace de l’équation avec second membre (terme source)
  3. Onde diffractée : perturbation de l’onde incidente par la présence de l’obstacle
• Solution élémentaire pour l’équation des ondes scalaire
  1. Rappel de la solution élémentaire du Laplacien
  2. Calcul de la solution élémentaire de l’équation de Helmholtz. Transformée de Fourier inverse, causalité, condition de radiation.

TD (§2.4 et §2.5 du poly)